C++ Lecture 02

       Programming with the Problem Analysis-coding-Execution Cycle

Programming is a process of problem solving. Different people use different techniques to solve problems. Some techniques are nicely outlined and easy to follow. They not  only solve the problem, but also give insight into how the solution was reached.  These problem-solving techniques can be easily modified if the domain of the  problem changes.

To be a good problem solver and a good programmer, you must follow good problem- solving techniques. One common problem-solving technique includes analyzing a problem, outlining the problem requirements, and designing steps, called an algorithm, to solve the problem.

Algorithm: A step-by-step problem-solving process in which a solution is arrived at in a finite amount of time.

In a programming environment, the problem-solving process requires the following three steps:

1.     Analyze the problem, outline the problem and its solution requirements, and design an algorithm to solve the problem.

2.     Implement the algorithm in a programming language, such as C++, and verify that the algorithm works.

3.     Maintain the program by using and modifying it if the problem domain changes.

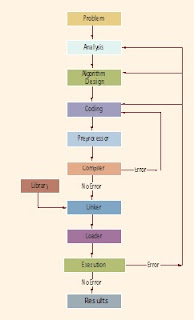
Figure 1-4 summarizes this three-step programming process.

FIGURE 1-4  Problem analysis–coding–execution cycle

To develop a program to solve a problem, you start by analyzing the problem. You then design the algorithm; write the program instructions in a high-level language, or code the program; and enter the program into a computer  system.

Analyzing the problem is the first and most important step. This step requires you to do the following:

1.     Thoroughly understand the  problem.

2.     Understand the problem requirements. Requirements can include whether the program requires interaction with the user, whether it manipulates  data whether it produces output, and what the output looks like. If the program manipulates data, the programmer must know what the data is and how it is represented. That is, you need to look at sample data. If the program produces output, you should know how the results should be generated and formatted.

3.     If the problem is complex, divide the problem into subproblems and repeat Steps 1 and 2. That is, for complex problems, you need to analyze each subproblem and understand each subproblem’s requirements.

After you carefully analyze the problem, the next step is to design an algorithm to solve the problem. If you broke the problem into subproblems, you need to design an algorithm for each subproblem. Once you design an algorithm, you need to check it for correctness. You can sometimes test an algorithm’s correctness by using sample data. At other times, you might need to perform some mathematical analysis to test the algorithm’s correctness.

Once you have designed the algorithm and verified its correctness, the next step is to convert it into an equivalent programming code. You then use a text editor to enter the programming code or the program into a computer. Next, you must make sure that the program follows the language’s syntax. To verify the correctness of the syntax, you run the code through a compiler. If the compiler generates error messages, you must identify   the errors in the code, remove them, and then run the code through the compiler again. When all the syntax errors are removed, the compiler generates the equivalent machine code, the linker links the machine code with the system’s resources, and the loader places the program into main memory so that it can be executed.

The final step is to execute the program. The compiler guarantees only that the program follows the language’s syntax. It does not guarantee that the program will run correctly. During execution, the program might terminate abnormally due to logical errors, such as division by zero. Even if the program terminates normally, it may still generate erroneous results. Under these circumstances, you may have to reexamine the code, the algorithm,     or even  the problem  analysis.

Your overall programming experience will be successful if you spend enough time to complete the problem analysis before attempting to write the programming instructions. Usually, you do this work on paper using a pen or pencil. Taking this careful approach to programming has a number of advantages. It is much easier to discover errors in a program that is well analyzed and well designed. Furthermore, a carefully analyzed and designed program is much easier to follow and modify. Even the most experienced programmers spend a considerable amount of time analyzing a problem and designing an algorithm.

Throughout this book, you will not only learn the rules of writing programs in C++, but you will also learn problem-solving techniques. Each chapter provides several programming exam- ples that discuss programming problems. These programming examples teach techniques of how to analyze and solve problems, design algorithms, code the algorithms into C++, and also help you understand the concepts discussed in the chapter. To gain the full benefit of this book, we recommend that you work through the programming examples at the end of each chapter.

Next, we provide examples of various problem-analysis and algorithm-design techniques.

Example 1

In this example, we design an algorithm to find the perimeter and area of a rectangle.

To find the perimeter and area of a rectangle, you need to know the rectangle’s length and width.

The perimeter and area of the rectangle are then given by the following formulas:

perimeter  =  2  · (length  +  width) area  =  length  · width

The algorithm to find the perimeter and area of the rectangle  is:

1.     Get the length of the rectangle.

2.     Get the width of the  rectangle.

3.     Find the perimeter using the following equation:

perimeter  =  2  · (length  +  width)

4.     Find the area using the following equation:

                area  =  length  · width

Example 2

In this example, we design an algorithm that calculates the sales tax and the price of an item  sold in a particular  state.

The sales tax is calculated as follows: The state’s portion of the sales tax is 4%, and the city’s portion of the sales tax is 1.5%. If the item is a luxury item, such as a car more than $50,000, then there is a 10% luxury   tax.

To calculate the price of the item, we need to calculate the state’s portion of the sales tax, the city’s portion of the sales tax, and, if it is a luxury item, the luxury tax. Suppose  salePrice  denotes  the  selling  price  of  the  item,  stateSalesTax  denotes the  state’s  sales  tax,  citySalesTax  denotes  the  city’s  sales  tax,  luxuryTax  denotes the luxury tax, salesTax denotes the total sales tax, and amountDue denotes the final price of the item.

To calculate the sales tax, we must know the selling price of the item and whether the item is    a  luxury item.

The stateSalesTax and citySalesTax can be calculated using the following formulas:

stateSalesTax  =  salePrice  · 0.04 citySalesTax  =  salePrice  · 0.015

Next, you can determine luxuryTax as follows:

·

if  (item  is  a  luxury  item) luxuryTax  =  salePrice     0.1

otherwise

luxuryTax  =  0

Next, you can determine salesTax as follows:

salesTax  =  stateSalesTax  +  citySalesTax  +  luxuryTax

Finally, you can calculate amountDue as follows:

amountDue  =  salePrice  +  salesTax

The algorithm to determine salesTax and amountDue is, therefore:

1.     Get the selling price of the item.

2.     Determine whether the item is a luxury  item.

3.     Find the state’s portion of the sales tax using the  formula:

stateSalesTax  =  salePrice  · 0.04

4.     Find the city’s portion of the sales tax using the  formula:

citySalesTax  =  salePrice  · 0.015

5.     Find the luxury tax using the following formula:

·

if  (item  is  a  luxury  item) luxuryTax  =  salePrice    0.1

otherwis luxuryTax  =  0

6.     Find salesTax using the formula:

salesTax  =  stateSalesTax  +  citySalesTax  +  luxuryTax

7.     Find amountDue using the formula:

amountDue  =  salePrice  +  salesTax

Example 3

In this example, we design an algorithm that calculates the monthly paycheck of a salesperson  at a local department  store.

Every salesperson has a base salary. The salesperson also receives a bonus at the end of each month, based on the following criteria: If the salesperson has been with the store for five years or less, the bonus is $10 for each year that he or she has worked there. If the salesperson has been with the store for more than five years, the bonus is $20 for each year that he or she has worked there. The salesperson can earn an additional bonus as follows: If the total sales made

by the salesperson for the month are at least $5,000 but less than $10,000, he or she receives a 3% commission on the sale. If the total sales made by the salesperson for the month are at least

$10,000, he or she receives a 6% commission on the sale.

To calculate a salesperson’s monthly paycheck, you need to know the base salary, the number of years that the salesperson has been with the company, and the total sales made by the sales- person for that month. Suppose baseSalary  denotes the base salary, noOfServiceYears denotes the number of years that the salesperson has been with the store, bonus denotes the bonus, totalSales denotes the total sales made by the salesperson for the month, and additionalBonus denotes the additional bonus.

You can determine the bonus as follows:

otherwise if  (noOfServiceYears  is  less  than  or  equal  to  five) bonus  =  10                                noOfServiceYears

bonus  =  20  · noOfServiceYears

Next, you can determine the additional bonus of the salesperson as follows:

if (totalSales is less than 5000) additionalBonus  =  0

otherwise

if (totalSales is greater than or equal to 5000  and

·

totalSales is less than 10000) additionalBonus  =  totalSales                                                    (0.03)

otherwise

additionalBonus  =  totalSales  · (0.06)

Following the above discussion, you can now design the algorithm to calculate a salesperson’s monthly  paycheck:

1.     Get baseSalary.

2.     Get noOfServiceYears.

3.     Calculate bonus using the following formula:

otherwise if  (noOfServiceYears  is  less  than  or  equal  to  five) bonus  =  10                               noOfServiceYears

bonus  =  20  · noOfServiceYears

4.     Get totalSales.

5.     Calculate additionalBonus using the following formula:

if (totalSales is less than 5000) additionalBonus  =  0

otherwise

if (totalSales is greater than or equal to 5000 and totalSales is less than 10000)

·

additionalBonus  =  totalSales           (0.03) otherwise

additionalBonus  =  totalSales  · (0.06)

6.     Calculate payCheck using the equation:

payCheck  =  baseSalary  +  bonus  +  additionalBonus

Example 4

In this example, we design an algorithm to play a number-guessing game.

The objective is to randomly generate an integer greater than or equal to 0 and less than 100. Then prompt the player (user) to guess the number. If the player  guesses  the  number  correctly, output an appropriate message. Otherwise,  check  whether  the  guessed number  is less than the random number. If the guessed number is less than the random number generated,  output  the  message,  ‘‘Your  guess  is  lower  than  the  number.  Guess  again!’’; otherwise, output the message, ‘‘Your guess is higher than the number. Guess again!’’. Then prompt the player to enter another number. The player is prompted to guess the random    number until the player enters the correct number.

The first step is to generate a random number, as described above. C++ provides the means to do so, which is discussed in Chapter 5. Suppose num  stands for the random  number and  guess  stands for  the number  guessed  by the player.

After the player enters the guess, you can compare the guess with the random number as follows:

if  (guess  is  equal  to  num)

Print  "You  guessed  the  correct  number." otherwise

if guess is less than num

Print  "Your  guess  is  lower  than  the  number.  Guess  again!" otherwise

Print  "Your  guess  is  higher  than  the  number.  Guess  again!"

You can now design an algorithm as follows:

1.     Generate a random number and call it num.

2.     Repeat the following steps until the player has guessed the correct number:

a.       Prompt the player to enter guess. b.

if  (guess  is  equal  to  num)

Print  "You  guessed  the  correct  number." otherwise

if guess is less than num

Print "Your guess is lower than the number. Guess again!" otherwise

Print "Your guess is higher than the number. Guess again!"

Example 5

There are 10 students in a class. Each student has taken five tests, and each test is worth 100 points. We want to design an algorithm to calculate the grade for each student, as well as the class average. The grade is assigned as follows: If the average test score is greater than or equal to 90, the grade is A; if the average test score is greater than or equal to 80 and less than 90, the grade is B; if the average test score is greater than or equal to 70 and less than 80, the grade is C; if the average test score is greater than or equal to 60 and less than 70, the grade is D; otherwise, the grade is F. Note that the data consists of students’ names and their test scores.

This is a problem that can be divided into subproblems as follows: There are five tests, so you design an algorithm to find the average test score. Next, you design an algorithm to determine the grade. The two subproblems are to determine the average test score and to determine the grade.

Let us first design an algorithm to determine the average test score. To find the average test score, add the five test scores and then divide the sum by 5. Therefore, the algorithm  is:

1.     Get the five test  scores.

2.     Add the five test scores. Suppose sum stands for the sum of the test scores.

3.     Suppose average stands for the average test score.  Then:

average  =  sum  /  5;

Next, you design an algorithm to determine the grade. Suppose grade stands for the grade assigned to a student. The following algorithm determines the grade:

if average is greater than or equal to 90 grade = A

otherwise

if average is greater than or equal to 80 and less than 90 grade = B

otherwise

if average is greater than or equal to 70 and less than 80 grade = C

otherwise

if average is greater than or equal to 60 and less than 70 grade = D

otherwise

grade  =  F

You can use the solutions to these subproblems to design the main algorithm as follows: (Suppose totalAverage stands for the sum of the averages of each student’s test average.)

1.     totalAverage = 0;

2.     Repeat the following steps for each student in the class:

a.       Get student’s name.

b.       Use the algorithm as discussed above to find the average test score.

c.       Use the algorithm as discussed above to find the grade.

d.       Update  totalAverage  by  adding  the  current  student’s  average  test score.

3.     Determine the class average as  follows:

classAverage  =  totalAverage  /  10

A programming exercise in Chapter 7 asks you to write a C++ program to determine the average test score and grade for each student in a class.